The shortest path problem in PHP: demystifying Dijkstra's algorithm

After a very long, but intensive, night, I’m happy to announce that Orient, the PHP library used to work with OrientDB, has integrated an interesting feature, an implementation of Dijkstra’s algorithm.

First of all, let me tell you that, as a pretty new implementation, I’m pretty sure a couple bugs will be spotted in the next days; second, the design of the algorithm and the entities connected to it could probably be better, so I recommend you to just take a look at the final result, ‘cause the internals will probably change a bit.

The problem

Given the following graph:

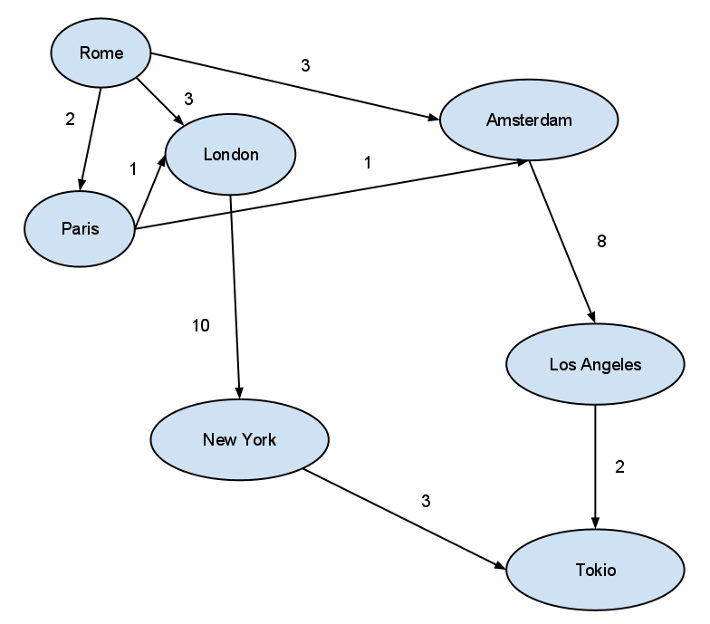
how do you calculate the best way to reach Tokio from Rome?

Ok, that’s easy, you can count with your mind when you have such a small dataset:

and as you probably already know, the simplest solution is to fly from Rome to Amsterdam To LA to Tokio: the distance is 13 (hours? 13k miles? No matter now).

(You can also reach Amsterdam via Paris, but we don’t care for the aim of this post)

The dataset grows… enter Orient

But as your dataset grows, you need to automate the process of finding shortest paths.

Just install Orient:

1

git clone [email protected]:congow/Orient.git

and create your path.php script, which should use the PSR-0 autoloader:

1
2
3
4
5
6
7
8

<?php

$classLoader = new SplClassLoader('Congow\Orient', __DIR__ . "/Orient/src");
$classLoader->register();

use Congow\Orient\Graph;
use Congow\Orient\Graph\Vertex;
use Congow\Orient\Algorithm;

At this point you might think that the algorithm’s implementation is pretty coupled with the rest of the library we’re developing, and you would be terribly wrong.

Take a look on how to create the graph

1
2
3

<?php

$graph = new Graph();

how to create vertices

1
2
3
4
5
6
7
8
9

<?php

$rome      = new Vertex('Rome');
$paris     = new Vertex('Paris');
$london    = new Vertex('London');
$amsterdam = new Vertex('Amsterdam');
$ny        = new Vertex('New York');
$la        = new Vertex('Los Angeles');
$tokio     = new Vertex('Tokio');

and how to connect vertices between themselves:

1
2
3
4
5
6
7
8
9
10
11

<?php

$rome->connect($paris, 2);
$rome->connect($london, 3);
$rome->connect($amsterdam, 3);
$paris->connect($london, 1);
$paris->connect($amsterdam, 1);
$london->connect($ny, 10);
$amsterdam->connect($la, 8);
$la->connect($tokio, 2);
$ny->connect($tokio, 3);

final step, add the vertices to the graph:

1
2
3
4
5
6
7
8
9

<?php

$graph->add($rome);
$graph->add($paris);
$graph->add($london);
$graph->add($amsterdam);
$graph->add($ny);
$graph->add($la);
$graph->add($tokio);

So, you have basically created some fixtures ( a fake graph, the one of the pictures above ), and we can finally calculate the shortest path from Rome to Tokio:

1
2
3
4
5
6
7
8

<?php

$algorithm = new Algorithm\Dijkstra($graph);
$algorithm->setStartingVertex($rome);
$algorithm->setEndingVertex($tokio);

echo $algorithm->getLiteralShortestPath() . ": distance " . $algorithm->getDistance();
// the real method to get the SP is $algorithm->solve(), the ones used above are for printing a nice result 

which will output:

1

Rome - Amsterdam - Los Angeles - Tokio : distance 13

If you have suggestions and questions, feel free to ask everything here; also, if you spot a bug, pull requests are welcome.